code.pyMEEP allows to create structures out of primitive objects viz sphere,cylinder cone, block and ellipsoid.  It is impossible to create hexagon shape with the direct use of primitive shapes. But if we cut a block with non-orthogonal planes we will get a triangle ¹ . Now since we can make triangular shapes, how can we get other shapes? A very nice post to create arbitrary shapes is written by Mr. Bala¹. As a beginner, I couldn't understand certain things in his post. In this post, I am going to explain how to create polygon in MEEP 2D out of primitive objects. I am using the method described in that post¹ .  I have also written a python script, in which you just feed in the coordinates and it will return you a meep code describing the structure. As an example, I'll make a hexagon shape in MEEP.

Delaunay Triangulation

In simple words, Delaunay triangulation is triangulation of set of points(that make the polygon).

With the help of Delaunay triangulation, we can deconstruct a polygon into a set of triangles.
Once we construct these triangles, we would get our structure 🙂
Step 1: Finding the triangles

Use delaunay triangulation to convert your polygon into set of triangles.

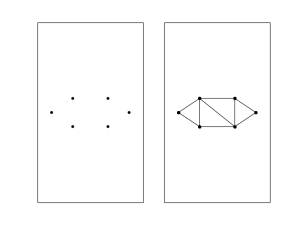
Step 2: Once you have found the triangles insert the properties of all the triangles in your meep code and execute to get your desired structure. 

Python Script:

I have written the following python script for convenience. Write down the points of your polygonal structure. It will return you MEEP code of the desired structure in a separate file name "coordinates". Install triangle package ^3,4 before you run the code. Enjoy 🙂
You can also download the script ,code.py .

 
import triangle
import triangle.plot
import numpy as np
import matplotlib.pyplot as plt
#define the points of the polygon
A = dict(vertices=np.array(((-5,4), (-11,0), (-5,-4), (5,4),(11,0),(5,-4))))
#triangulate
B = triangle.triangulate(A)
#plot the figure 
triangle.plot.compare(plt, A, B)
plt.show()
a=B['vertices'] #vertices
b=B['triangles'] # getting the indices of vertices
n=len(b) #no. of triangles
#declaring the constants
e=12 #epsilon
z=-5.0 #point in another plane
temp=np.zeros((n,3))
f = open('coordinates', 'w') #file to write meep code
f.write("(set! geometry (list \n") #first line in meep to create geometrical objects
for i in range(0, n):
   print "vertices of %d th triangle" %(i+1)   
   for j in range(0,3):
     print "x coordinate is" + str(a[b[i][j]][0])+ " y coordinate is " + str (a[b[i][j]][1])
     temp[j][0]=a[b[i][j]][0]
     temp[j][1]=a[b[i][j]][1]  
   #defining the centers    
   xc=(temp[0][0]+temp[1][0]+temp[2][0])/2
   yc=(temp[0][1]+temp[1][1]+temp[2][1])/2
   #direction vectors
   e1x=temp[0][0]
   e1y=temp[0][1]
   e2x=temp[1][0]
   e2y=temp[1][1]
   e3x=temp[2][0]
   e3y=temp[2][1] 
   #magnitude of direction vectors
   s1=np.square(e1x)+np.square(e1y)+np.square(z)
   s2=np.square(e2x)+np.square(e2y)+np.square(z)    
   s3=np.square(e3x)+np.square(e3y)+np.square(z) 
   f.write("(make block (center " +str(xc) +" " +str(yc) +" " +str((-z/2)) +") (material ( make        dielectric (epsilon " + str(e)+ " ))) (size  (sqrt "+str(s1)+") (sqrt "+str(s2)+ ") (sqrt  "+str(s3)+")  ) (e1 " +str(e1x)+" "+ str(e1y)+" " +str(-z)+ " ) (e2" +str(e2x)+" "+ str(e2y)+" "    +str(-z)+ ") (e3 "+str(e3x)+" "+ str(e3y)+" " +str(-z)+ ") ) \n")     
f.write(" ))")
f.close()  

References

1. http://juluribk.com/2011/05/10/arbitrary-2d-shapes-in-meep/
2. http://ab-initio.mit.edu/wiki/index.php/Meep
3. http://dzhelil.info/triangle/
4. http://www.cs.cmu.edu/~quake/triangle.html